Vectors in R2 and R3
>
This week we learned about vectors in 2/3 dimensional space.
We are taking a more geometric and physics based approach as opposed
to an abstract mathematical approach.
What is a vector (in R2 and R3)? Well a vector is a displacement with
some magnitude (length) and direction relative towards the coordinate axes.
Since this vector is just this displacement,
it can be translated anywhere in the coordinate system and be the same vector.

Vector Addition
This definition becomes very useful for basic operations like adding two vectors together. This can be accomplished by placing the tail of one vector at the tip of the other and then drawing the vector that goes from the tail of the first o the tip of the second. Also, addition of these vectors is commutative meaning that $\vec{a} + \vec{b} = \vec{b} + \vec{a}$
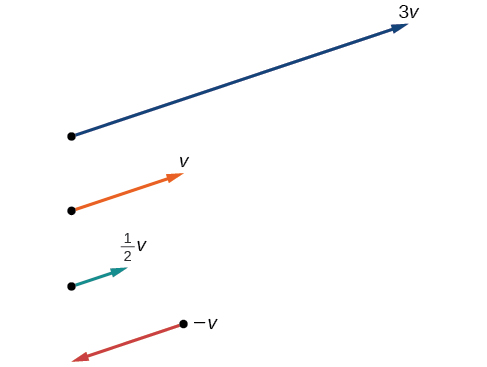
Vector Scaling
Vectors can also be multiplied by scalars or scaled by some factor. This can done by multiplying the scalar through to each component, and is one way to help think about vector subtraction. You can scale a vector by negative on then add it to another vector meaning that $\vec{a} - \vec{b} = \vec{a} + -1 \cdot \vec{b}$
Vector Length
The length of a vector, also called the magnitude, is the distance from the tail to the tip. This can be found using the Pythagorean theorem by making the vector itself the hypotenuse and each component another side of the triangle. This can the be expanded to three dimensions by adding a third component. The length is denoted as $length(\vec{a}) = ||\vec{a}||$.
Vector Normalization and Unit Vectors
Vector normalization is the process of normalizing a vector or scaling that vector so that it has a length of 1. When this is done the resulting vector is called a unit vector which is denoted with a '^' over it, also called a 'hat'. This is done by scaling the vector by the reciprocal of the length meaning that the unit vector for som vector $\hat{a} = \frac{\vec{a}}{||\vec{a}||}$. This process is very useful for representing vectors in different coordinate spaces.

Vector Dot Product and projection
The dot product is one of the multiplication-like operations that can be performed on two vectors. It takes two vectors and returns a scalar result. It can be performed by multiplying the components in a specific direction and summing all of them together. The formula looks like: $\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z$ Interestingly the length of a vector can be described as the square root of it dotted with itself meaning $length(\vec{a}) = \sqrt{\vec{a} \cdot \vec{a}}$. Vector projection is a way of expressing changing the direction of a vector to be parallel to another. In other words we can take a vector, say $\vec{a}$, and project it onto (or in the direction of) another vector, say $\vec{b}$. The resultant vector, lest call it $\vec{c}$, has the same magnitude of $\vec{a}$ but is now in the direction of $\vec{b}$. This can be done by multiplying $\vec{a}$ by a unit vector in the direction of $\vec{b}$.